Tree Layout Algorithm

Contexte de création

Créé le 10 juin 2021 pour le jeu "Alternia".

Mon objectif

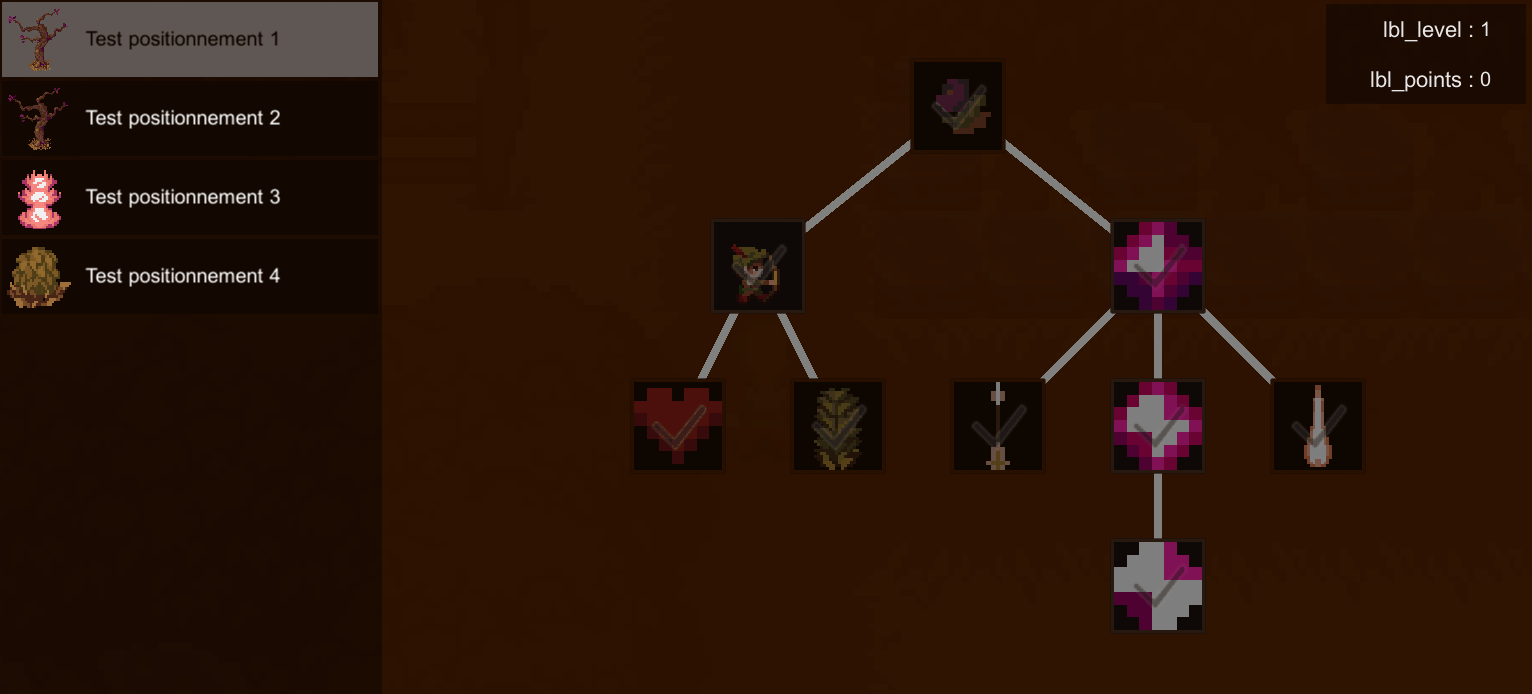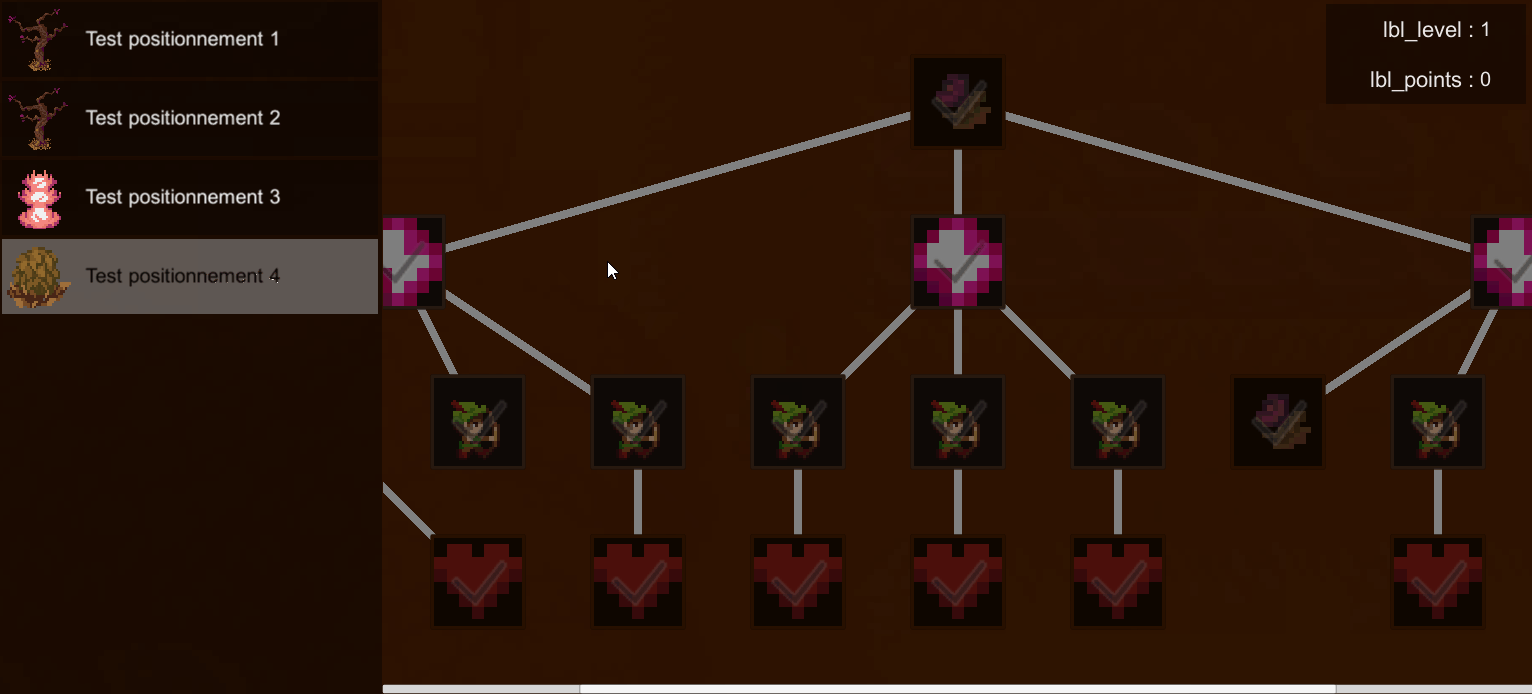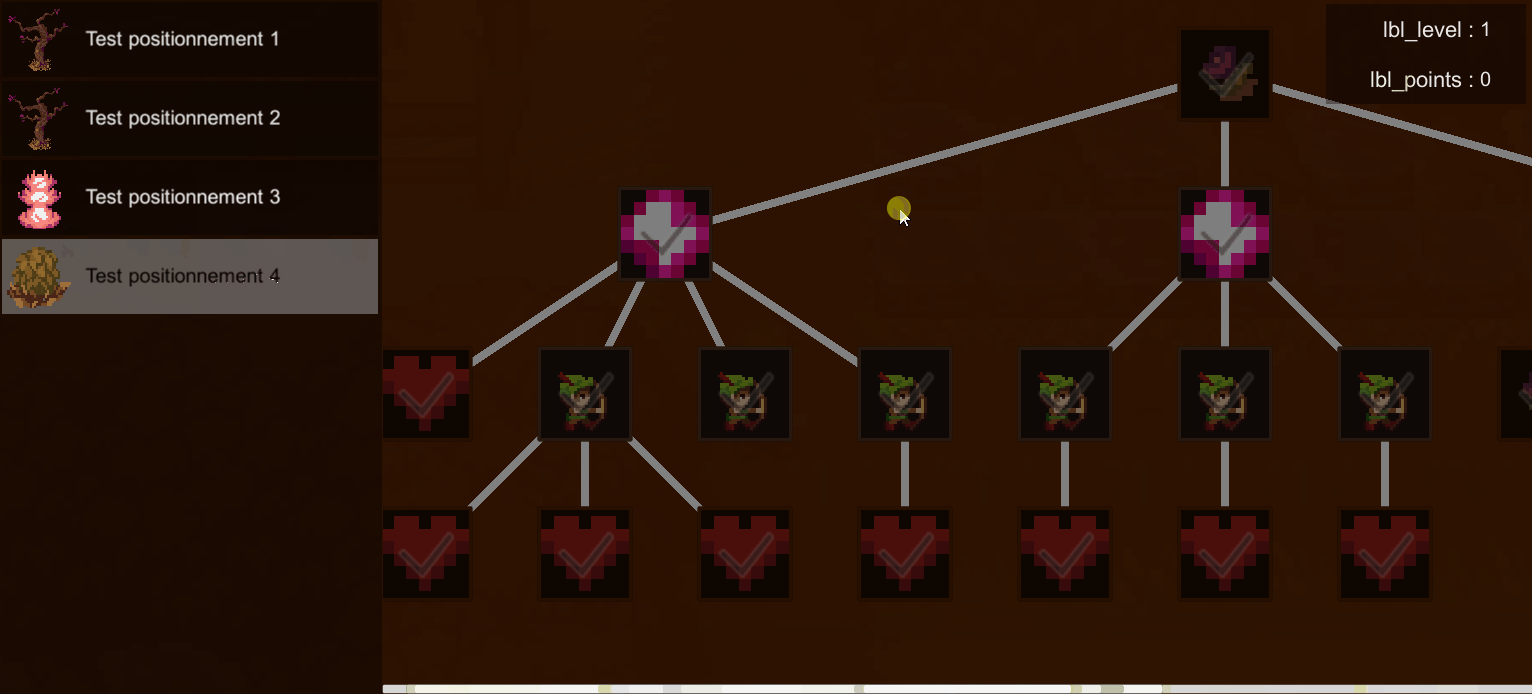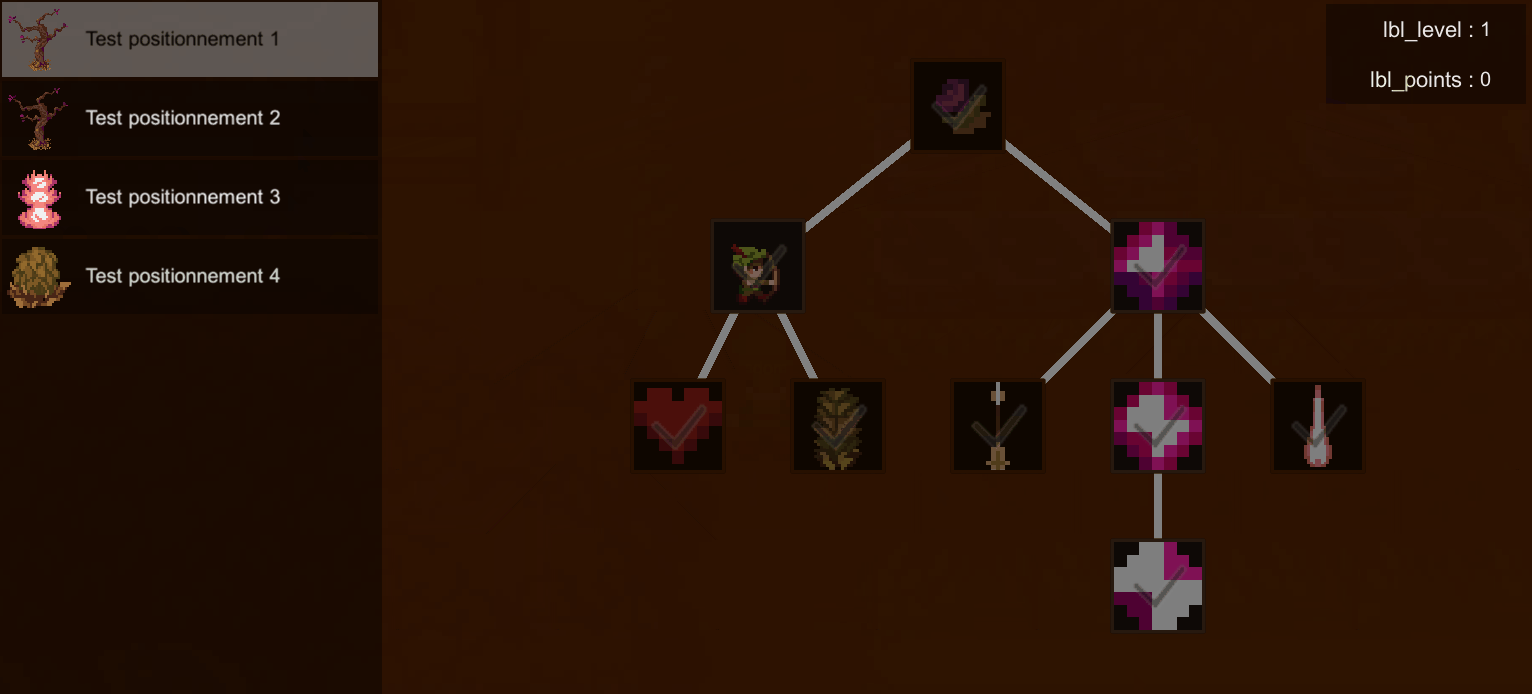
Mon objectif pour ce projet était de réaliser un algorithme viable permettant de positionner les noeuds d'un arbre de données de façon intelligible en une seule traversée, afin de simplifier le rendu de l'arbre de compétences du jeu "Alternia" tout en réduisant au maximum le coût en ressources de ce processus.

Description du projet

Prérequis

La fonction nécessite au moins 3 paramètres :

• le noeud à positionner,
• la position horizontale la plus à gauche de l'arbre,
• la profondeur du noeud actuel.

ainsi qu'un moyen de stocker la position horizontale la plus à droite pour chaque niveau de profondeur (un dictionnaire utilisant la profondeur comme clé par exemple).

Explication de l'algorithme

Pour pouvoir effectuer une seule traversée de l'arbre sans perdre en simplicité, on effectue une traversée en post-ordre (enfants puis racine).

Si le nombre d'enfants du noeud actuel est supérieur à zéro :

• Pour chaque enfant :
  • Si l'enfant actuel n'est pas le premier, qu'il a lui-même plus d'un enfant et que l'enfant précédent n'a pas d'enfant&nbsp: la position horizontale cible est la position horizontale de l'enfant précédent.
  • Sinon, si la dernière position horizontale à la profondeur suivante (profondeur actuelle + 1) est définie et la position horizontale reçue en paramètre est inférieure à cette dernière + la largeur de l'enfant actuel&nbsp: la position horizontale cible est la dernière position horizontale à la profondeur suivante + la largeur de l'enfant actuel.
  • Finalement, on positionne chaque enfant du noeud actuel avec comme paramètres la position horizontale cible et la profondeur suivante.
• Ensuite, on récupère les positions horizontales respectives de l'enfant le plus à gauche et de l'enfant le plus à droite,
• Puis on définit la position horizontale du noeud actuelle au centre des deux positions préalablement enregistrées.

Sinon, si la dernière position horizontale pour la profondeur actuelle est définie et la position horizontale reçue en paramètre est inférieure à cette dernière&nbsp: on définit la position horizontale cible à la dernière position horizontale pour la profondeur actuelle.

Sinon, si la dernière position horizontale pour la profondeur précédente (profondeur actuelle - 1) est définie et la position horizontale reçue en paramètre est inférieure à cette dernière&nbsp: on définit la position horizontale cible à la dernière position horizontale pour la profondeur précédente.

Pour finir, on définit la dernière position horizontale pour la profondeur actuelle ainsi que la position horizontale du noeud actuelle à la position horizontale cible et la position verticale à la profondeur actuelle multipliée par la hauteur d'un noeud.

Exemple d'utilisation

Pour faciliter la compréhension de ce dernier, j'ai également réalisé un exemple d'utilisation en python (le jeu est codé en C# mais j'ai choisi le python pour l'exemple pour sa simplicité de lecture et de transposition dans un autre langage).

Pseudo-code de l'algorithme

Dictionary<int, float> lastXAtDepth

FUNCTION Instantiate(node, xPosition = 0, depth)

    IF depth < 0 THEN
        RAISE EXCEPTION : Depth shouldn't be negative
    END IF

    IF node.childCount > 0 THEN
        FOR i IN range(0, node.childCount) DO
            child = node.children[i]

            IF i > 0 AND child.childCount > 1 AND node.children[i - 1].childCount EQUALS 0 THEN
                xPosition = node.children[i - 1].xPosition
            ELSE IF lastXAtDepth CONTAINS KEY depth + 1 AND xPosition &lt lastXAtDepth[depth + 1] + child.width
                xPosition = lastXAtDepth[depth + 1] + child.width
            END IF

            Instantiate(child, xPosition, depth + 1)
        END FOR

        minX = node.children[0].xPosition
        maxX = node.children[node.childCount - 1].xPosition

        xPosition = (minX + maxX) / 2
    ELSE IF lastXAtDepth CONTAINS KEY depth AND xPosition < lastXAtDepth[depth] THEN
        xPosition = lastXAtDepth[depth]
    ELSE IF lastXAtDepth CONTAINS KEY depth - 1 AND xPosition < lastXAtDepth[depth - 1] THEN
        xPosition = lastXAtDepth[depth - 1]
    END IF

    lastXAtDepth(depth) = xPosition
    node.xPosition = xPosition
    node.yPosition = depth * nodeHeight

END FUNCTION

Ce que j'ai appris

Lors de la création de ce projet, j'ai été amené à réaliser un algorithme facile à faire évoluer et à utiliser en prenant en compte des limitations techniques précises. Cet exercice m'a permis d'améliorer mes capacités d'analyse et de résolution de problème ainsi que d'optimisation pouvant s'avérer indispensables durant le développement d'une application.

Libre à vous d'utiliser cet algorithme comme bon vous semble et d'y apporter votre touche personnelle tant que vous pensez à me créditer !

Tags

Unity, C#, Algorithme, Programmation UI